今天我们来看一个简单的数学问题： 已知$a<b$，求$a^b=b^a$的正整数解的个数。

由于上面的等式中有幂的运算，应该可以想到在两边同时取对数将其转换为乘法： } $$\log(a^b)=\log(b^a) \rightarrow b\log(a)=a\log(b) \rightarrow \frac{\log(a)}{a}=\frac{\log(b)}{b}$$

经过上述的转换，题目转变成了：已知$f(x)=\frac{\log(x)}{x}$, 求$f(a)=f(b)$的正整数解的个数。所以接下来需要研究一下$f(x)$的性质了。先对$f(x)$求导：

$$\frac{df}{dx}=\frac{1-\log(x)}{x^2}$$

由此可见，令$f'(x)=0$，得到唯一驻点$x=e$，当$0<xe$，$f(x)$单调递减。所以可以得到$0<ae$。也因为$a$和$b$都为正整数，所以$a$只可能是$1$或者$2$。但是$f(1)=0$且$f(x)$不存在其它任何和x轴的交点，所以$a$只可能等于$2$。稍微试验便可发现$b$等于$4$。

最终结果为该等式正整数解的个数为1个，即$a=2$，$b=4$。

由图1 中$f(x)=\frac{log(x)}{x}$的函数图便可清楚的看出：

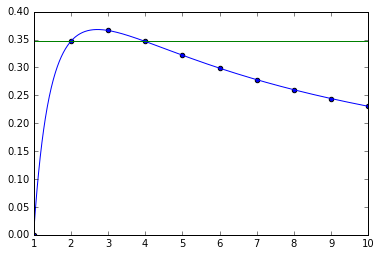
（以上$log$均为自然对数）